Title: Determine where two circles intersect in Python

[A program showing where two circles intersect]

This example shows one method for finding where two circles intersect in Python. If you don't like math, skip to the code below.
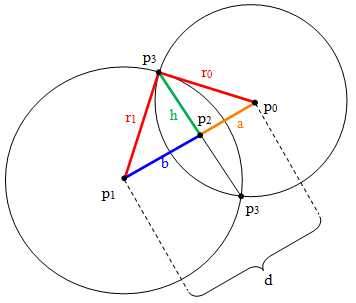example Consider the figure on the right showing two circles with radii r₀ and r₁. The points p₀, p₁, p₂, and p₃ have coordinates (x₀, y₀) and so forth.

Let d be the distance between the circles' centers so [Equation] . Solving for a gives . Now there are three cases:

If d > r₀ + r₁: The circles are too far apart to intersect.
If d < |r₀ - r₁|: One circle is inside the other so there is no intersection.
If d = 0 and r₀ = r₁: The circles are the same.
If d = r₀ + r₁: The circles touch at a single point.
Otherwise: The circles touch at two points.

(Note: It's hard to draw two circles that touch at exactly one point. To test those cases, you may need to write some code that perfectly positions the second circle.)

The Pythagorean theorem gives:

So:

Substituting [Equation]

and multiplying this out gives:

The -b² terms on each side cancel out. You can then solve for b to get:

Similarly:

All of these values are known so you can solve for a and b. All that remains is using those distances to find the points p₃. If a line points in direction <dx, dy>, then two perpendicular lines point in the directions <dy, -dx> and <-dy, dx>. Scaling the result gives the following coordinates for the points p₃:

Be careful to notice the ± and ∓ symbols.

The Code

The following code shows the find_circle_circle_intersections method that the program uses to find intersections.

def find_circle_circle_intersections(center0, radius0, center1, radius1): '''Find the 0, 1, or 2 points where the circles intersect.''' # Find the distance between the centers. dx = center0[0] - center1[0] dy = center0[1] - center1[1] dist = math.sqrt(dx * dx + dy * dy) # See if the circles are so far apart they don't intersect. if dist > radius0 + radius1: print('Circles too far apart, no intersections') return () # See if one circle contains the other. if dist < abs(radius0 - radius1): print('One circle inside the other, no intersections') return () # See if the circles coincide. if math.isclose(dist, 0) and math.isclose(radius0, radius1): print('Circles coincide, no intersections') return () # Otherwise we have 1 or 2 intersections. # Find a and h. a = (radius0 * radius0 - radius1 * radius1 + dist * dist) / (2 * dist) h = math.sqrt(radius0 * radius0 - a * a) # Find P2. cx2 = center0[0] + a * (center1[0] - center0[0]) / dist cy2 = center0[1] + a * (center1[1] - center0[1]) / dist # Get the points P3. intersection1 = ( cx2 + h * (center1[1] - center0[1]) / dist, cy2 - h * (center1[0] - center0[0]) / dist) intersection2 = ( cx2 - h * (center1[1] - center0[1]) / dist, cy2 + h * (center1[0] - center0[0]) / dist) # See if we have 1 or 2 solutions. print(f'{intersection1 = }') print(f'{intersection2 = }') if math.isclose(intersection1[0], intersection2[0]) and \ math.isclose(intersection1[1], intersection2[1]): # One intersection. They're the same point. return (intersection1,) return (intersection1, intersection2)

This code follows the explanation above.

Download the example to see additional details. When you click and drag twice to define two circles, the program uses the find_circle_circle_intersections method to find the points of intersection (if any) and draws them.