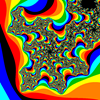
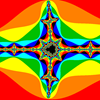
Title: Draw the Mandelbrot set and zoom in on areas in Python and tkinter

The Mandelbrot set uses an iterated equation to calculate colors for the points in a region. The equation is:

Z(n) = Z(n-1)² + C

It can be shown that, if the magnitude of Z(n) ever exceeds 2, then it eventually diverges towards infinity.

To find the color for the point (x, y) in world coordinates, the program sets Z(0) = 0 and C = x + y * i. It then generates values for Z(n) until Z(n)'s magnitude exceeds 2 or the program reaches some predetermined maximum number of iterations. At that point, the program uses the number of iterations it performed to assign the point's color. For example, if the program is using k colors and it performed j iterations, then it assigns the point color number j % k.

This example is similar to Let the user zoom on a picture in Python and tkinter. That example draws a PIL image and lets you click and drag to select areas to zoom in on. See that example for most of the drawing and zooming details.

This example just uses a different method to draw its PIL image. The following code draws the Mandelbrot set.

def draw(self): '''Draw an image.''' # Set scale factors for drawing. self.x_scale = (self.vxmax - self.vxmin) / (self.wxmax - self.wxmin) self.y_scale = (self.vymax - self.vymin) / (self.wymax - self.wymin) # Make an image to fit the viewport. mode = 'RGB' image_wid = self.vxmax - self.vxmin image_hgt = self.vymax - self.vymin bg_color = (0, 0, 0) self.image = Image.new(mode, (image_wid, image_hgt), bg_color) # Access the image's pixels. self.pixels = self.image.load() # Get the viewport's bounds in world coordinates. w_vxmin, w_vymin = self.d_to_w(0, 0) w_vxmax, w_vymax = self.d_to_w(image_wid - 1, image_hgt - 1) # Work until |Zn| >= escape_radius; escape_radius = 2.0 z0 = 0 + 0j max_iterations = 64 # Define the colors. black = ( 0, 0, 0) red = (255, 0, 0) orange = (255, 128, 0) yellow = (255, 255, 0) dark_green = ( 0, 192, 0) cyan = ( 0, 255, 255) blue = ( 0, 0, 255) colors = ( black, red, orange, yellow, dark_green, cyan, blue ) # Loop over the pixels. for x in range(image_wid): for y in range(image_hgt): # Calculate this point's color. re, im = self.d_to_w(x, y) c = re + im * 1j z = z0 iteration = 0 while ((iteration < max_iterations) and (abs(z) < escape_radius)): # Calculate Z(clr). z = z * z + c iteration += 1 # Set the pixel's color. if (iteration >= max_iterations): color = black else: color = colors[iteration % len(colors)] self.pixels[x, y] = color # Convert the PIL image into an ImageTk.PhotoImage. self.photo_image = ImageTk.PhotoImage(self.image) # Display the result. self.canvas.delete('all') self.display_image = self.canvas.create_image(0, 0, anchor=tk.NW, image=self.photo_image)

The program then defines the escape radius, Z0, and the maximum number of iterations. I set max_iterations to 64. If you make this number larger, the program takes longer to draw the Mandelbrot set but it provides more detail. This is particularly useful if you zoom in closely on an area.

The code defines the colors that it will use for the set and then starts looping over the image's pixels.

For each pixel at position (x, y) in the PIL image, the program converts x and y into world coordinates. It then sets C equal to x + y * i and enters a while loop where it calculates the next Z(n) value. If the program has exceeded the maximum number of iterations or if the magnitude of Z(n) exceeds the escape radius, then program breaks out of its while loop.

The program then assigns the pixel a color. If we exceeded the maximum number of iterations, the pixel is black. Otherwise the program takes the number of iterations mod the number of colors and uses that color number.

The code finishes by converting the PIL image into a ImageTk.PhotoImage and displaying it as in the previous example.

Download the example to see additional details.