Title: Solve the recurrence relation that calculates the size of the Hilbert and Sierpinski fractal curves

$[Solve the recurrence relation that calculates the size of the Hilbert and Sierpinski fractal curves]$

The post Use induction to calculate the number of segments in a Hilbert curve fractal proves that the width of a Hilbert curve of depth N is 2^N - 1. Similarly, the post Use induction to calculate the number of segments in a Sierpinski curve fractal proves that the width of a Sierpinski curve of depth N is 2^{N + 2} - 2.

Those posts prove that the equations work, but how do you figure out what those equations are in the first place?

One approach is to stare at the numbers until either the solution pops out or you give up in despair. Fortunately, there's a more systematic approach that works for this kind of recurrence relationship.

The Hilbert Curve

A recurrence relationship is a set of equations that gives a value in terms of previous values. For example, if H(N) is the width of a Hilbert curve of depth N, then it's fairly easy to see that H(N) = 2 * H(N - 1) + 1.

In this example, the size of the curve roughly doubles each time you increase the curve's depth because H(N) involves 2 * H(N - 1). When that occurs, you should suspect that the equation for a depth N curve involves 2 to the power of N, possibly with some constant added to the power and possibly with some constant term added or subtracted from the result.

To figure out exactly what the equation looks like, build a table holding depths, values of corresponding powers of 2, and the curve's width. Here's the table for the Hilbert curve.

Depth N	1	2	3	4	5
2^N	2	4	8	16	32
Width	1	3	7	15	31

Now compare the powers of 2 in the second row to the curve widths in the third row. It doesn't take long to notice that each width is one less than its corresponding power of 2. In other words, H(N) = 2^N - 1.

That's all there is to it!

Before you continue reading, you might like to try the same calculation for the Sierpinski curve. See the following posts for information about that curve.

Hint: You have to compare each curve width to a power of two that is not necessarily directly over that curve width.

*** Give it a try now ***

The Sierpinski Curve

Here's the table for the Sierpinski curve.

Depth N	1	2	3	4	5	6
2^N	2	4	8	16	32	64
Width	6	14	30	62	126	254

This one isn't as obvious as the table for the Hilbert curve, but if you compare curve widths to powers of two, you'll notice that the width for depth N is 2 less than the power of two in column N + 2. In other words, if S(N) is the curve's width, then S(N) = 2^{N + 2} - 2.

Voilà!

Number of Lines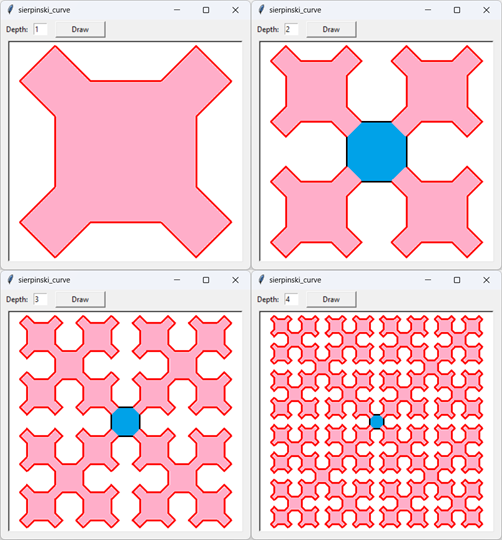

They key to the previous calculations is to make a table and compare the widths to the powers of 2. The only other trick is knowing that it's powers of two that you should look at. You know it's powers of 2 because H(N) involves 2 times H(N - 1). Similarly, S(N) involves 2 times S(N - 1).

Let's look at another problem that doesn't involve powers of 2.

Take a look at the picture of the Sierpinski curves on the right and count the number of line segments that make up each curve. For example, the depth 1 curve consists of 16 segments.

The depth 2 curve includes 4 copies of the depth 1 curve. To build the depth 2 curve, we remove 1 line segment from each of the depth 1 curves and then we add 4 new segments to connect the sub-curves. More generally, if Ss(N) is the number of line segments in a Sierpinski curve of depth N (Ss stands for "Sierpinski segments"), then Ss(N + 1) = 4 * Ss(N) - 4 + 4 = 4 * Ss(N).

This time Ss(N + 1) involves 4 times Ss(N), so we should look at powers of 4. Here's the table for this recurrence.

Depth N	1	2	3	4	5	6
4^N	4	16	64	256	1024	4096
# Segments	16	64	256	1024	4096	16,384

This time it's easy to see that the number of line segments for a depth N curve is the same as the power of two in column N + 1 so Ss(N) = 4^{N + 1}.

Summary

To find the equation for the recurrence X(N), determine how many copies of X(N) go into making up X(N + 1) and call that value P. For example, in the Hilbert and Sierpinski curves widths, P = 2. For the number of line segments in a Sierpinski curve, P = 4.

Then make a table holding N, P^N, and X(N). Compare the values of P^N and X(N) to see how to calculate X(N).